| Theory |
|---|
 The overlap of two circles
The overlap of two circles The order-two diagram (left) consists of two intersecting circles, producing a total of four regions, A, B, A ∩ B, and Ø (the empty set, represented by none of the regions occupied).
The order-two diagram (left) consists of two intersecting circles, producing a total of four regions, A, B, A ∩ B, and Ø (the empty set, represented by none of the regions occupied).Here, A ∩ B denotes the intersection of sets A and B. The formula for the calculation of the intersection between two circles (with different radii R and r) is: A = r2cos-1((d2+r2-R2)/2dr)+R2cos-1((d2+R2-r2)/2dR) -1/2sqrt((-d+r+R)(d+r-R)(d-r+R)(d+r+R)). 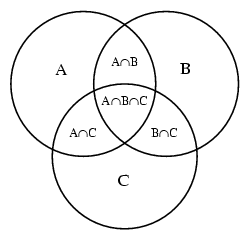 The overlap of three circles
The overlap of three circlesThe order-three diagram (right) consists of three symmetrically placed mutually intersecting circles comprising a total of eight regions. The regions labeled A, B, and C consist of members which are only in one set and no others, the three regions labelled A ∩ B, A ∩ C, and B ∩ C consist of members which are in two sets but not the third, the region A ∩ B ∩ C consists of members which are simultaneously in all three, and no regions occupied represents Ø. The intersection between three circles can be approached by using the two-circle-formula for each of the three pairs. Please note that is not possible to have the three-circle intersection proportional as well. The computer script on this site calculates the distances between the centers of the three circles, and the angles between these three lines, in such a way that the overlapping areas of the circles correspond to the numbers that are put in by the user.  An example
An exampleLet's take a look at these three sets of letters: Set A: a, d, f, h, m, r, s, u, z, B, E, G, J, K, M, O, R, U, X, Y, Z Set B: b, c, g, h, l, o, q, r, t, w, y, A, D, E, H, I, O, P, Q, T, W, Y, Z Set C: c, e, h, j, k, n, p, C, F, G, I, L, N, P, S, T, U, V, Y Set A has a size of 21. Set B contains 23 letters, set C is the largest set with 19 letters. The overlap between set A and B (A ∩ B) is 6 (h, r, E, O, Y and Z). A ∩ C is 4 (h, G, U and Y), B ∩ C is 6 (c, h, I, P, T and Y). The intersection between all three circles (A ∩ B ∩ C) is 2 (h and Y). Then the corresponding proportional Venn Diagram as drawn by VennDiagram.tk will look like the image on the right. |